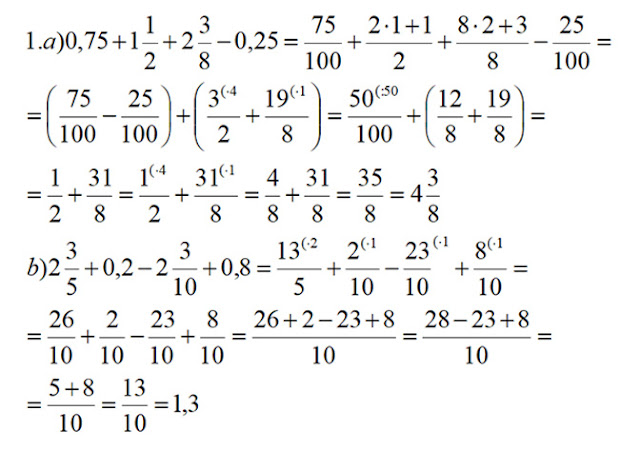matematika-lazic

1. Објављујем домаћи који је тачно урадила Сара Стојановић 8/1. Послали су домаћи још Лазар Поповић 8/4 (тачно) и неко ко се није потписао (тачно), а урадили су још и Данило Николић и Петар Булић 8/1. АКО ЈЕ ЈОШ НЕКО СЛАО ДОМАЋИ НЕКА НАПИШЕ У КОМЕНТАРУ. Решење је (5,5; -0,5) или (11/2; -1/2) 2. Ако нисте погледајте нову лекцију са РТС-а https://rtsplaneta.rs/video/show/1352972/ 3. Сада да објасним графичку методу решавања система једначина. Идеја: Нацртати обе праве (једначине) и видети да ли се секу – ако се секу онда је то решење и очитати га са графика. ПОДСЕТИ СЕ: Експлицитни облик је кад је само y на левој страни y = kx + n Дефиниција: Систем графички решавамо тако што прво изразимо обе једначине у експлицитном облику. y = k 1 x + n 1 (прва једначина, означаваћемо бројем 1) y = k 2 x + n 2 (друга једначина, означаваћемо бројем 2) Затим обе праве/једначине нацртамо (претходна лекција, цртање линеарне функције, помоћу две тачке) и можемо им...

1. Анализа домаћег задатка: домаћи су урадили само Софија и Лазар (Поповић?) из 8/4. Доле је дато решење Софије Марковић. 2x+y=13 3x-2y=2 --------------- y=13-2x 3x-2y=2 --------------- y=13-2x 3x-2×(13-2x)=2 -------------------------- y=13-2x 3x-26+4x=2 --------------------- y=13-2x 7x-26=2 ---------------- y=13-2x 7x=2+26 ---------------- y=13-2x 7x=28 ---------------- y=13-2x x=28/7 ---------------- y=13-2x x=4 ---------------- y=13-2×4 x=4 ---------------- y=5 x=4 Rešenje datog sistema je uredjeni par (x,y)=(4,5). 2. Ако нисте погледали сада погледајте лекцију преко РТС-а https://rtsplaneta.rs/video/show/1350545/ 3. Нека појашњења лекције: како се систем решава помоћу методе супротних коефицијената (још се зове и Гаусова метода). Дефиниција 1: Ако уз x или y имамо супротне коефицијенте (бројеве), нпр. у првој је -5x а у другој једначини је +5x, онда систем можемо да решимо методом супротних коефицијената: једну једначину задржимо, а друга ће бити кад САБЕРЕМО ОБЕ...

1. Анализа домаћег задатка: доста вас је послало решења, али мислим да је само један ученик (Магдалена Гашовић) имао оба тачна решења (ако грешим исправите ме у коментарима, ако је још неко послао оба тачна), највише вас је имало по један тачан. Ево детаљног решења оба примера: (Пример под b сте могли и да групишете посебно разломке а посебно децимални запис, па би било 0,2+0,8=1,0=1 итд.) 2. Ако нисте погледали – одгледајте сада лекцију преко РТС-а: https://rtsplaneta.rs/video/show/1350524/ Ако можете, урадите пројектни задатак који је задала наставница преко РТС-а. Ако нисте у стању – урадите домаћи задатак који вам ја задајем. ДОМАЋИ ЗАДАТАК: 1. Израчунај колико износи 1/2 од 1/6. (УПУТСТВО:  1/2  од x је  1/2  ⋅ x) 2. Ученик је имао штап канап дужине 0,6 метара, а онда га је скратио за једну четвртину његове дужине. Колико је сада дуг штап. (УПУТСТВО: Претвори све у „обичне“ разломке a/b и реши.) 3.* Сабери збир и...

1. Решењ е претходног домаћег :   Тачан одговор је c)   (1, -2) Tребало je заменити  x,y у сваки пример, а  под c добијамо ОБЕ тачне једначине: 2x + y = 0 x - y = 3 2*1 + (-2) = 0 1 - (-2) = 3 2 - 2 = 0 1 + 2 = 3 0 = 0 3 = 3 Зато је уређени пар (1, -2) решење, јер смо добили на крају ТАЧНО када смо заменили x,y 2.  Ако нисте погледали одгледајте лекцију на сајту РТС-а https://mojaskola.rtsplaneta.rs/show/1348873/532/os8-matematika-resavanje-sistema-dve-linearne-jednacine-sa-dve-nepoznate-2-cas За домаћи вам је задала из Збирке за завршни испит задатак број 202 , па то урадите и тамо имате решење па проверите. 3.   Наставница је објаснила и методу замене коју смо ми већ помињали. Подсећам шта је метода замене. Дефиниција : Метода замене састоји се у томе што из једне једначине система изразимо или x или y и тај израз заменимо у другу једначину. Обично замењујемо, ако постоји, "само"  x или y (не 3 x или -2y). ДОМА...

1. Решења претходног домаћег. Понављам и задатке и дајем решења:   Напомињем да и на Интернету остаје записано ко је радио домаће задатке а ко није. 2. Наставница је у првој лекцији преко телевизије задала отприлике овакав задатак: Канап има дужину 2/3 метра. Како да од њега тачно добијемо 1/2 метра? Она је узела канап, поделила га на пола, па још на пола (и тако добила четвртину) и онда је ту последњу четвртину "одузела" од целе дужине. Тако ће доиста добити тачно 1/2 метра, а ево математичког објашњења. Она од целе дужине канапа одузима 1/4 тог истог канапа. 3. Ако нисте погледали одгледајте лекцију на сајту РТС-а https://mojaskola.rtsplaneta.rs/show/1347151/527/os5-matematika-brojevni-izrazi-svojstva-operacije-sabiranja Напомињем да је наставница доста брзо урадила доста различитих задатака: неке ствари још нисмо радили, тако да НЕ БРИНИТЕ ако вам сада није све јасно, а гледајте да што више ствари сами схватите. 4. Наставница је на крају решил...

1. Погледајте лекцију на сајту РТС-а ако већ нисте. https://mojaskola.rtsplaneta.rs/show/1347044/517/os8-matematika-sistemi-dve-linearne-jednacine-sa-dve-nepoznate 2. Пошто је лекција практично обнављање оног што смо радили, и за домаћи је задато оно што смо ми већ радили, урадите следећи задатак за домаћи Домаћи задатак: 1. Одреди који је уређени пар бројева решење система и зашто: 2x + y = 0 x - y   = 3 a)  (1, 2) b)  (2, 1) c)  (1, -2) d)  (-2, 1) 3. Ко уради први домаћи, нека остави решења у коментару испод. Да би коментар био објављен, наведите своје име, презиме и одељење. 4. Не заборавите да можете за завршни испит да вежбате онлајн на адреси  http://www.zavrsniispit.matf.bg.ac.rs/

1. Пре саме лекције на РТС-у потребна су додатна објашњења, јер се не поклапа скроз рад преко РТС-а са нашим планом, нити ће се скроз поклапати. 2. Дакле, прво треба добро схватити појам децималног записа разломка, што иде у наставку. ДЕЦИМАЛНИ ЗАПИС РАЗЛОМКА Дефиниција 1:  Разломке чији су имениоци  декадне цифре (10, 100, 1000 ...) зваћемо ДЕЦИМАЛНИ разломци. Дефиниција 2: Код децималног записа разломака део до зареза зовемо ЦЕО ДЕО, а део после ДЕЦИМАЛЕ (децимални део) …abc,def… где је: цифра стотина – a цифра десетица – b цифра јединица – c (ТО ЈЕ ЦЕО ДЕО) цифра десетих – d цифра стотих – e цифра хиљадитих – f ... ( ТО ЈЕ ДЕЦИМАЛНИ ДЕО) Дефиниција 3 : Децимални запис разломка има онолико места иза зареза колико нула има његов именилац. ЗАДАЦИ: 3. Ко уради први домаћи, нека остави решења у коментару испод. Да би коментар био објављен, наведите своје име, презиме и одељење. 4. Сада погледајте л...

КРАЈ РЕДОВНЕ НАСТАВЕ НА ДАЉИНУ!!! 29. 5. 2020.  Лекција  / 5. разред /  Осна симетрија 29. 5. 2020.  Лекција  / 8. разред / Припрема за завршни испит - Обрада података _______________________________________________________ 28. 5. 2020.  Лекција  / 5. разред /  Примена симетрала дужи и угла (вежбање) 28. 5. 2020.  Лекција  / 8. разред / Припрема за завршни испит - Мерење _______________________________________________________ 26. 5. 2020.  Лекција  / 5. разред /  Симетрала дужи и угла (вежбање) 26. 5. 2020.  Лекција  / 8. разред / Припрема за завршни испит - Геометрија (2) _______________________________________________________ 25. 5. 2020.  Лекција  / 5. разред /  Симетрала угла (обрада) 25. 5. 2020.  Лекција  / 8. разред / Припрема за завршни испит - Геометрија (1) _____________________________________________________...